feedback patterns / deutscher Text
Muster aus der Schleife / visuelle Rückkopplungen
Thema
70er Jahre: Ein TV-Monitor zeigt das Bild einer VHS Kamera an. Was geschieht wenn man die Kamera auf diesen TV Monitor richtet?
Wie können solche Effekte digital nachgebildet werden?
Wie können wir mit Algorithmen ähnliche Effekte erzeugen?
GPN Foto Regeln
Auf der GPN Menschen nur photographieren wenn diese vorher ihr Einverständnis gegeben haben.
Offizieller Text: https://entropia.de/GPN23:FAQ Fotografieren
Vorbilder
- analoges TV Equipment
- Eine Kamera welche ihr eigenes Bild aufnimmt.
- analoge modulare Synthesizer für Sound
- voltage controlled oscillators
- no-input-mixer
Begriffe
Schleife / Rückkopplung
- Ein Verfahren immer wieder auf seine Ergebnisse anwenden.
Signal / Datenfluss
- Bilddaten die durch eine Filterkette laufen.
Intern / Extern
- intern: Bilddaten mit Algorithmen direkt auf der Grafikkarte manipulieren.
- extern: Monitor - Kamera - Schleifen.
- extern: In der optischen Achse befinden sich Spiegel, Gläser, Folien …
“Studio”
 Zwei Bildschirme, die Kamera ist auf den linken Bildschirm ausgerichtet.
Unterschiedliche Software Tools.
Zwei Bildschirme, die Kamera ist auf den linken Bildschirm ausgerichtet.
Unterschiedliche Software Tools.
 Monitor - Kamera - Schleife. Simpler Effektfilter.
Monitor - Kamera - Schleife. Simpler Effektfilter.
 Monitor - Spiegel - Kamera - Effektfilter - Schleife.
Ein nanoKONTROL2 MIDI Controller um die Parameter des Effektfilters zu verändern.
Monitor - Spiegel - Kamera - Effektfilter - Schleife.
Ein nanoKONTROL2 MIDI Controller um die Parameter des Effektfilters zu verändern.
 Der Plattenspieler als Drehteller, Kamera von Oben, Unterschiedliche Lichtquellen, Sensoren.
Der Plattenspieler als Drehteller, Kamera von Oben, Unterschiedliche Lichtquellen, Sensoren.
 Ein kleiner “Infinity Mirror Room” siehe: Yayoi Kusama
Ein kleiner “Infinity Mirror Room” siehe: Yayoi Kusama
Eigene Software
“analog Not analog”
Die meisten Beispiele in diesem Workshop sind mit aNa erstellt.
- Video Synthesizer und Manipulator.
- algorithmisch Formen und Farbverläufe erzeugen.
- Prototyping eines visuellen Datenflusses
- kann über Open Sound Control gesteuert werden.
- ist live coding fähig.
- ist aufwendig zu installieren, steile Lernkurve voraus.
“Glich camera / Loop camera / Blend camera”
Zum experimentieren für unterwegs.
- Drei Webseiten welche den Kamera-Stream manipulieren.
- Läuft auch auf Smartphones.
- Einfach zu bedienen.
Bestandteile des Workflows
- Das Setting für die photographische Aufnahme
- plus eine Kette von Effektfiltern
- plus die visuelle Rückkopplung
- optional Algorithmen für geometrische Verzerrungen, Perlin Noise, Kantenerkennung, …
- optional optische Gläser, Spiegel, Gruscht, …
Datenfluss
Direkter Datenfluss mit Effektfilter
- Farben drehen / HSV Farbmodell
- Fehlabtastung der Farbkanäle des Inputs
- Pixelation
- Geometrie verzerren
- … Spiegelachsen, Kanten hervorheben, …
Ein simplifizierendes sehr buntes Beispiel:

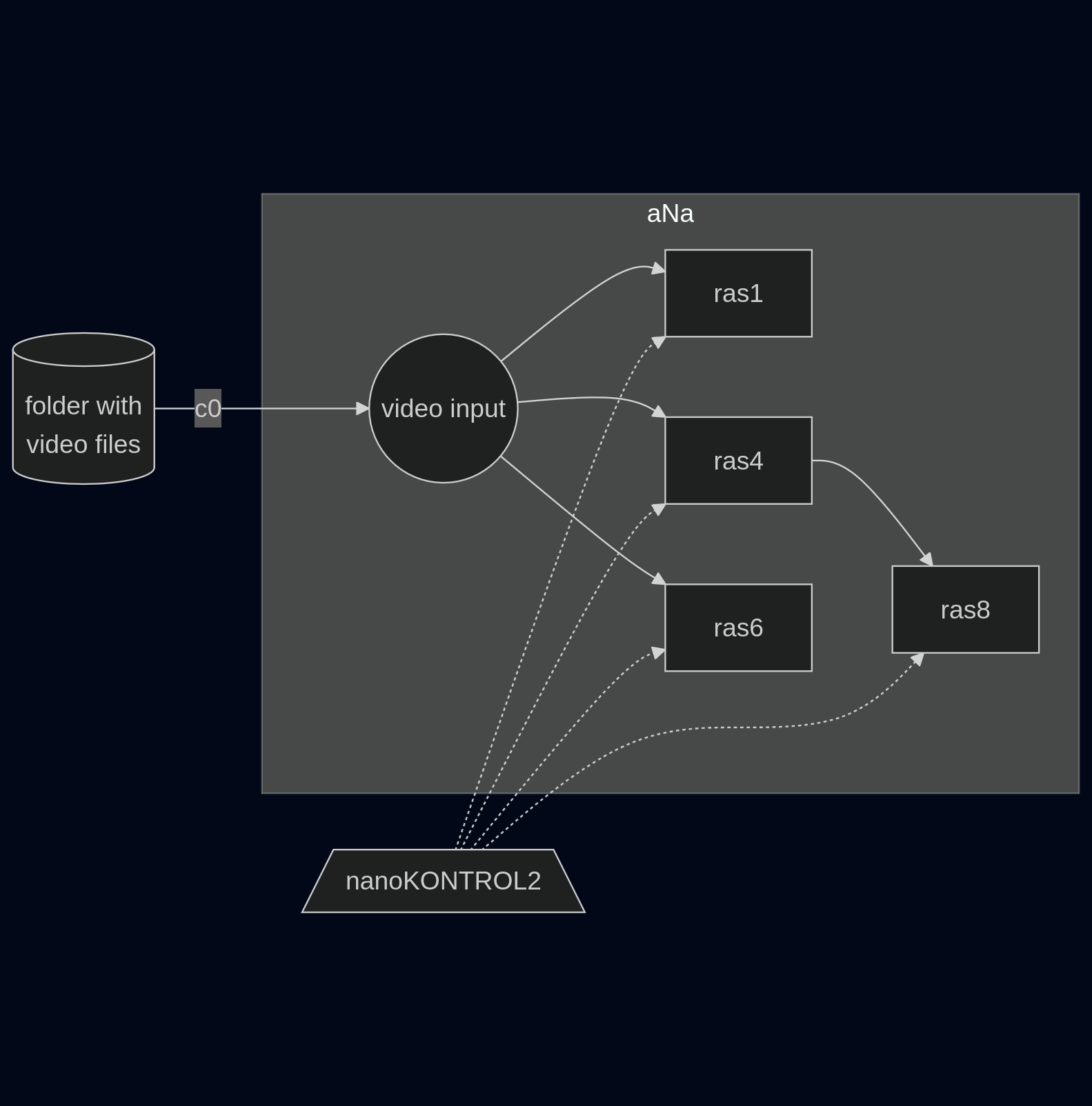
(ns lv.demo)
(use 'lv.core)
(layout "vertical" [mov0 ras1 ras4 ras6 ras8])
(render)
(movie "4movies/*.mp4")
; movie as input stream
(rgb :mov0 [c0, c1, c2 c3]
(sy 1.5)
(rgb c0.rgb)
)
; color shift
(hsv :ras1 [mov0]
(h (+ ks0 mov0.h))
(s (* 2 ks1 mov0.s))
(v (* 2 ks2 mov0.v))
)
; trichrom
(rgb :ras4 [mov0]
(r mov0.r)
(ty (* 0.3 ks4))
(g mov0.g)
(ty (* 0.3 ks4))
(b mov0.b)
)
; pixelate
(rgb :ras6 [mov0]
(pixelate-x (* ks6 1024))
(rgb mov0.rgb)
)
; distored geometry
(rgb :ras8 [ras4]
(tx (snoise x y))
(ty (snoise y x ))
(rgb ras4.rgb)
)
; ks0 0.44531
; ks1 0.57812
; ks2 0.66406
; ks4 0.4375
; ks5 0.58594
; ks6 0.4375
Mixer
Mixer zum überblenden zweier Bild-Signale.
Ähnlich zur Doppelbelichtung auf einem analogen Film.
Ähnlich zum Blend Modes zwischen Layern in einem Fotobearbeitungsprogrammen.
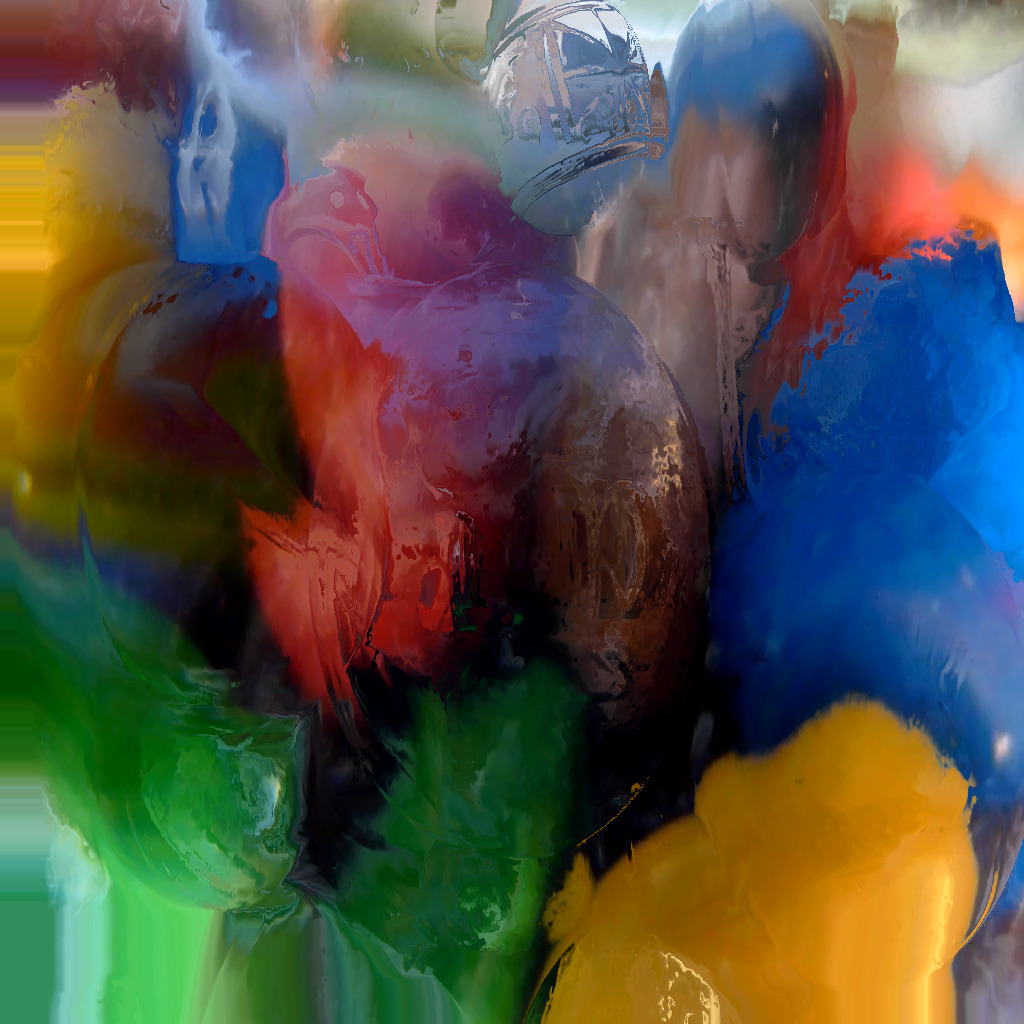
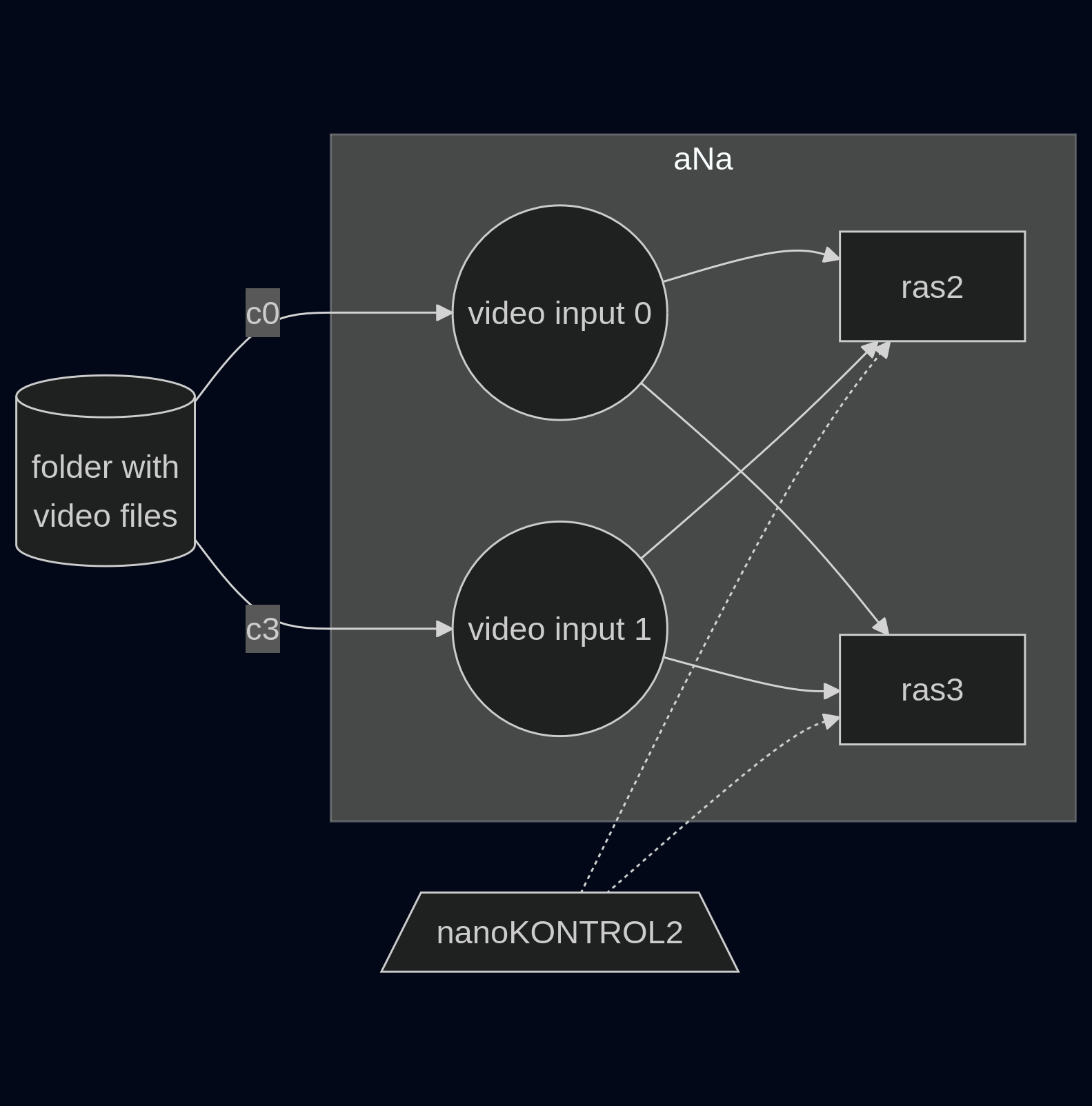
(ns lv.demo)
(use 'lv.core)
(layout "vertical" [mov0 mov1 ras2 ras3])
(render)
(movie "4movies/*.mp4")
; movie as input stream
(rgb :mov0 [c0, c1, c2 c3]
(sy 1.5)
(rgb c0.rgb)
)
; movie as input stream
(rgb :mov1 [c0, c1, c2 c3]
(sy 1.5)
(rgb c3.rgb)
)
; mixing by multiplication
(rgb :ras2 [mov0 mov1]
; (rgb (mix mov0.rgb mov1.rgb ks0))
(rgb (* mov0.rgb mov1.rgb))
)
; distorted geometry
(rgb :ras3 [mov0 mov1]
(tx (* ks1 -0.3 mov0.g))
(ty (* ks2 0.3 mov0.r))
(rgb mov1.rgb)
)
Keys als “Weichen”
Dies ist direkt aus dem analogen TV inspiriert.
luma key: Dort wo Signal 1 heller ist als ein Schwellwert wird Signal 2 weiter gegeben.chroma key: Dort wo Signal 1 eine bestimmte Farbe aufweist wird Signal 2 weiter gegeben. (green screen)
Hier ein “luma key” Beispiel. Die Helligkeit steuert pro Pixel die Auswahl welches Signal weitergegeben wird.

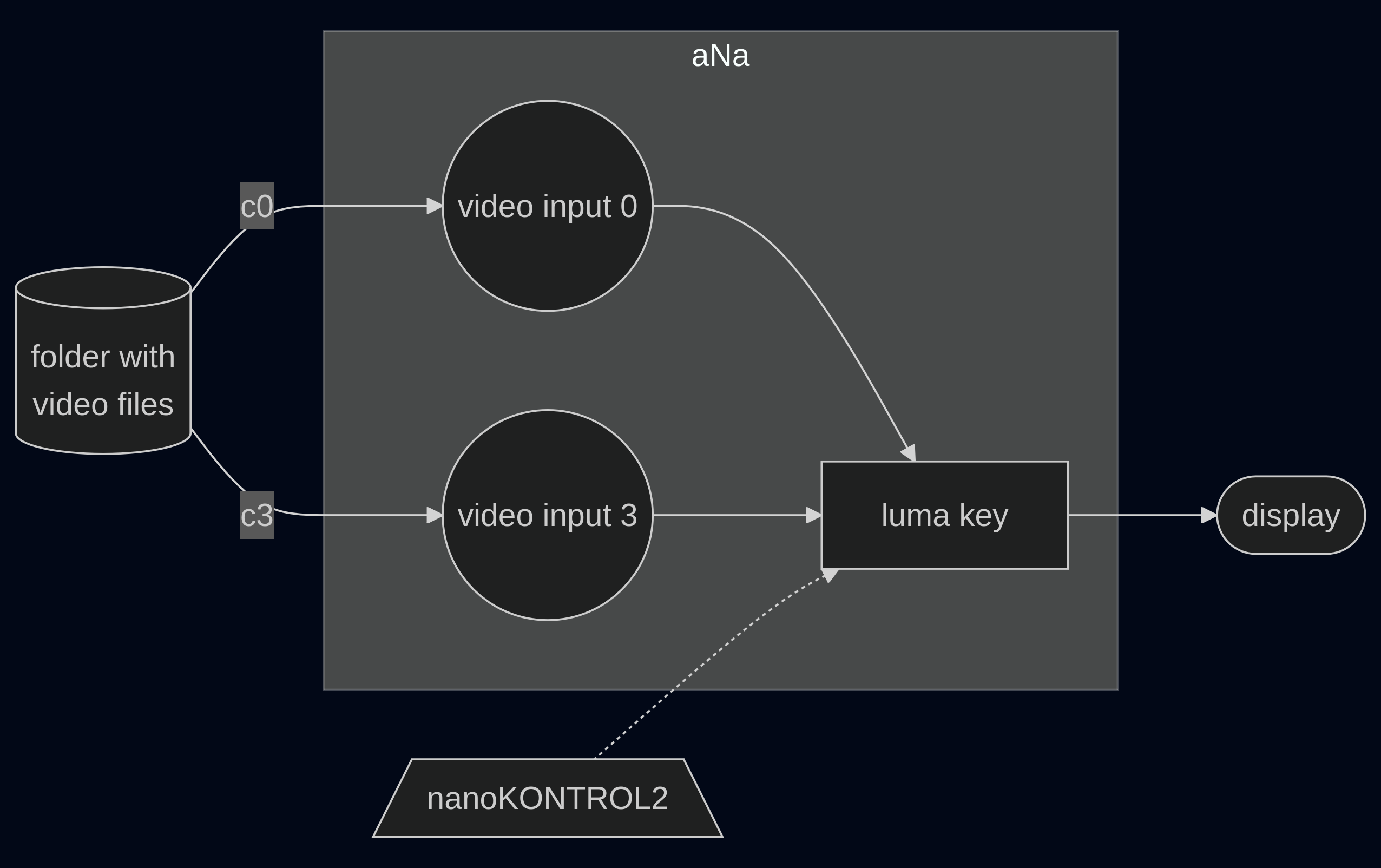
(ns lv.demo)
(use 'lv.core)
; (layout "vertical" [mov0 mov1 ras2 ras3])
(layout "vertical" [mov0 mov1 ras2 ])
(render)
(movie "4movies/*.mp4")
; movie as input stream
(rgb :mov0 [c0, c1, c2 c3]
(sy 1.5)
(rgb c2.rgb)
)
; movie as input stream
(rgb :mov1 [c0, c1, c2 c3]
(mirror)
(kaleid 5)
(sy 1.5)
(rgb c3.rgb)
)
; luma key
(hsv :ras2 [mov0 mov1]
(hsv (pos? (- mov0.v (* 0.3 ks0)) mov0.hsv mov1.hsv))
)
; ks0 0.26562
Interne Rückkopplungen
Die Rückopplung findet direkt im Speicher der Grafikkarte statt. “Digitales Bildsignal”.
Es gibt mindestens:
- einen Eingang um Bilddaten in das System zu bringen. (Initiator oder Seed)
- einen zusätzlichen Bild-Speicher.
- eine Rückkopplung des Bild-Signals.
- einen Mixer oder Key.
Es gibt optional:
- einen oder mehrere Effektfilter.
Initiator / Seed
Irgendwie müssen Daten ins System kommen die dann in die Rückkopplungsschleife fließen.
Initiator in digitalen Systemen
- den Stream der USB-Kamera ins System bringen.
- oder ein einfaches Muster per Algorithmus erzeugen.
Initiator in analogen Systemen
- den Stream der VHS-Kamera ins System bringen.
- das thermische Rauschen der Transistoren eines Audio Mixer verwenden. no-input-mixer
Algorithmus als Initiator
Beispiel für eine digitale Rückkopplung. Ein simples Streifenmuster wird durch die Rückkopplung zu einem komplexen Muster.
In der Rückkopplungsschleife werden die Koordinaten der Pixel rotiert, skaliert und verschoben. (Affine Transformation)
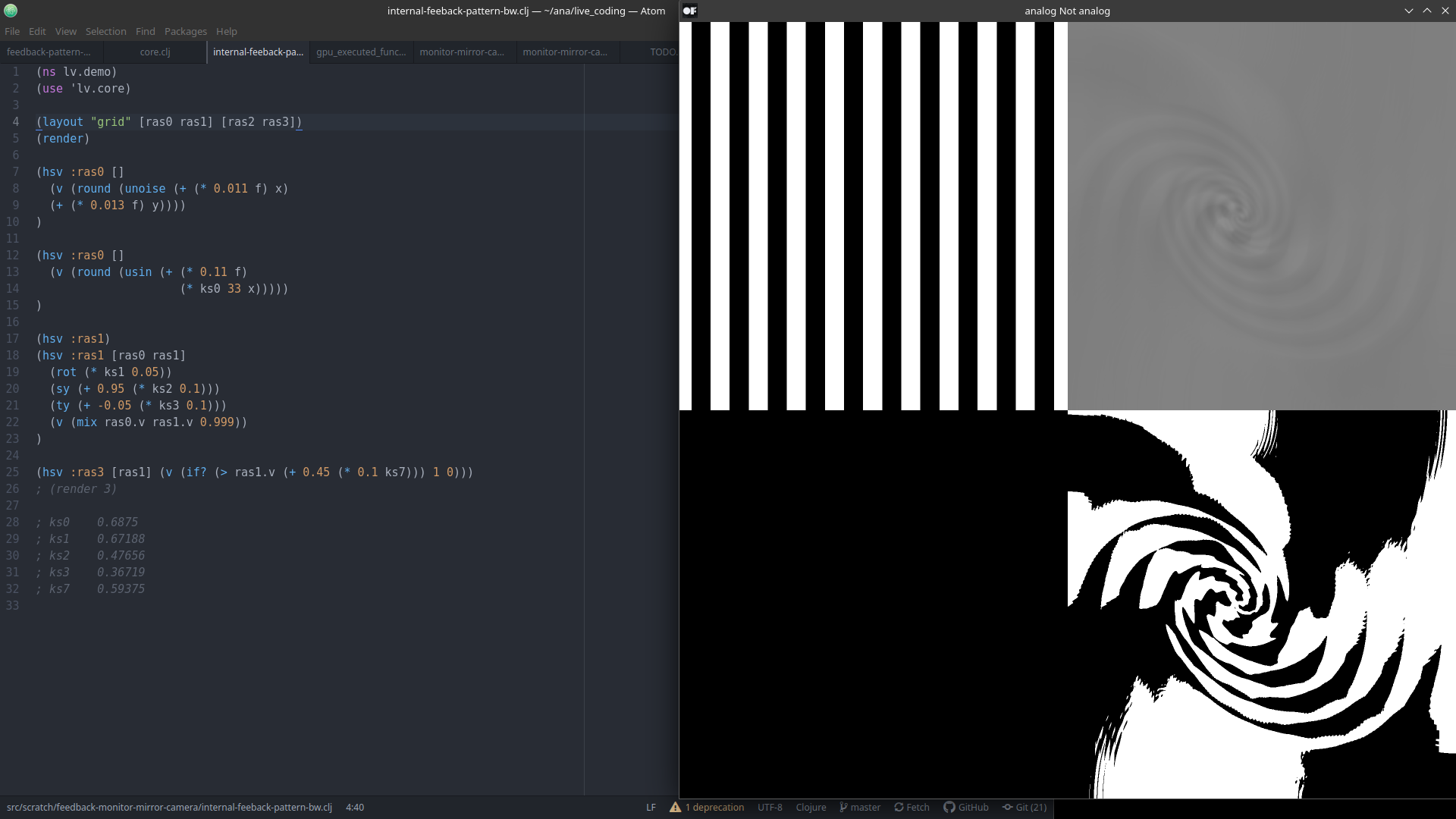
Zusammenspiel der Bestandteile:
ras0Muster erzeugenras1Speicher für Rückkopplung- geometrische Transformation
- und Mixer
ras3nachgeschalteter Effektfilter
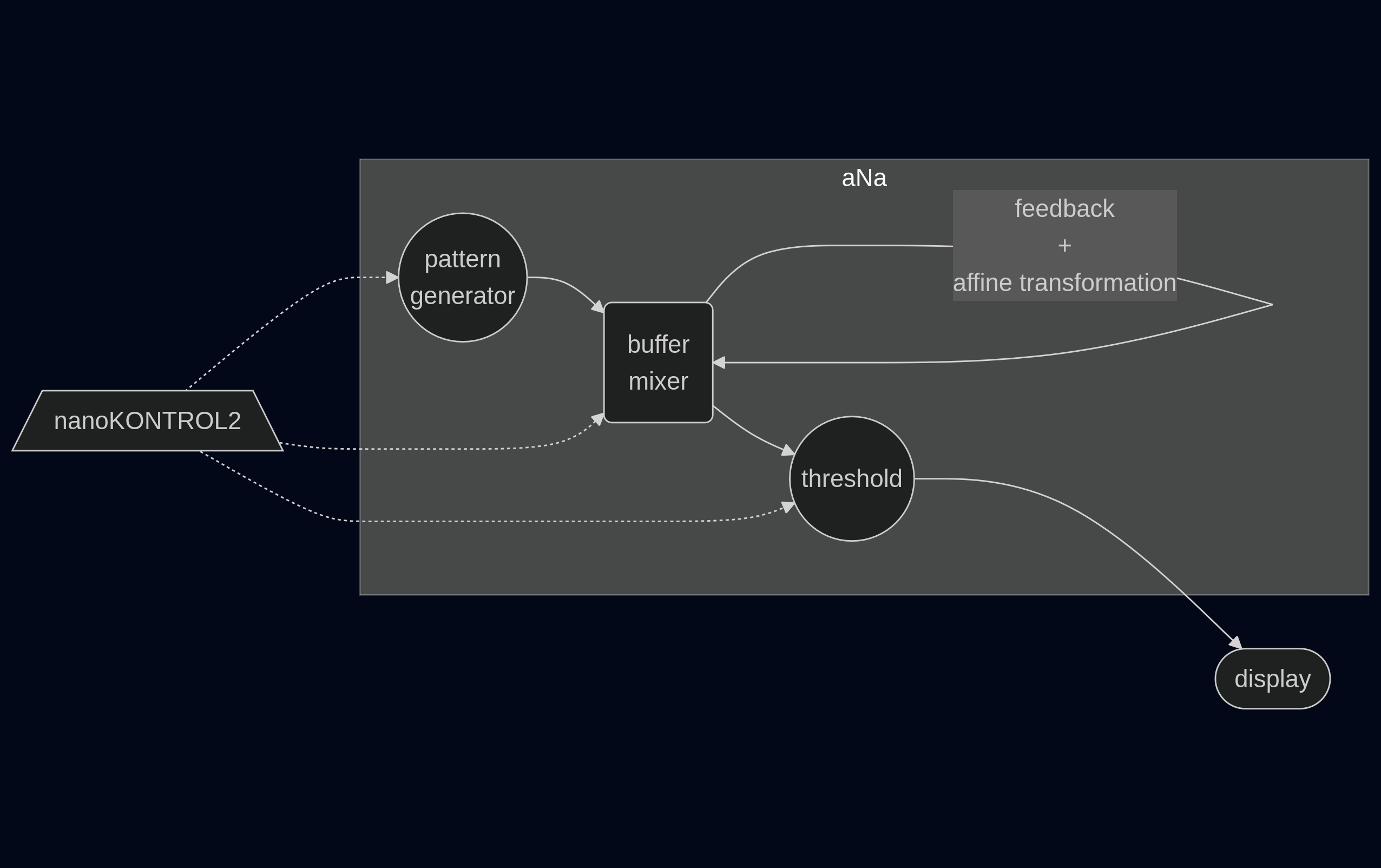
(ns lv.demo)
(use 'lv.core)
(layout "grid" [ras0 ras1] [ras2 ras3])
(render)
(hsv :ras0 []
(v (round (usin (+ (* 0.11 f)
(* ks0 33 x)))))
)
(hsv :ras1 [ras0 ras1]
(rot (* ks1 0.05))
(sy (+ 0.95 (* ks2 0.1)))
(ty (+ -0.05 (* ks3 0.1)))
(v (mix ras0.v ras1.v 0.999))
)
(hsv :ras3 [ras1]
(v (if? (> ras1.v (+ 0.45 (* 0.1 ks7))) 1 0))
)
; ks0 0.6875
; ks1 0.67188
; ks2 0.47656
; ks3 0.36719
; ks7 0.59375
Beispiel mit bunten Streifen.
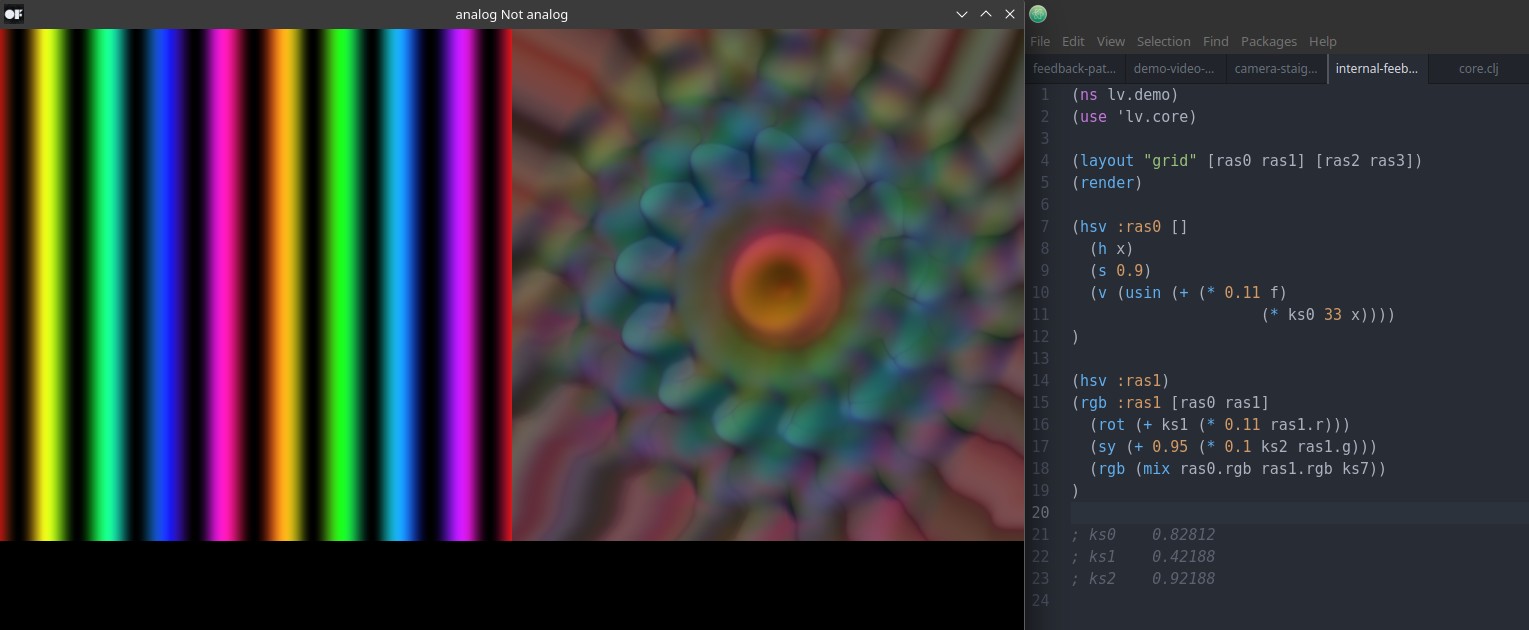
Kamera-Stream oder Video als Initiator
Achtung: diese Muster sind nicht zuverlässig zu reproduzieren. Es sind eher Zufallsfunde.
Red blue internal feedback loop.
A camera stream is feeding an internal feedback loop.
Zusammenspiel der Bestandteile:
mov0Live Stream der Kameraras1Speicher für Rückkopplung + geometrische Transformationras3nachgeschaltete Gammakorrektur
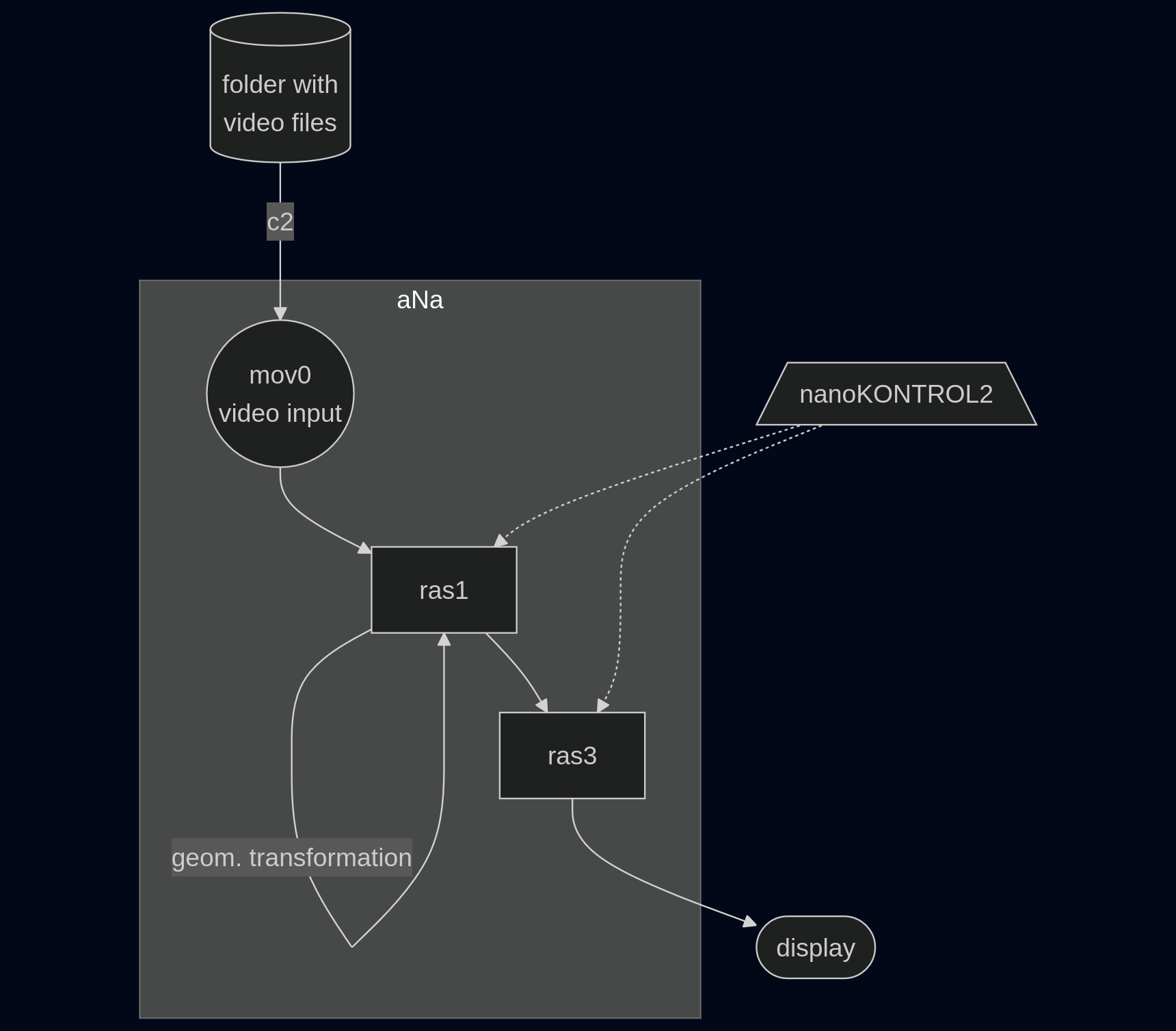
(ns lv.demo)
(use 'lv.core)
(layout "grid" [mov0 ras1] [ras2 ras3])
(render)
(movie "4movies/*.mp4")
; movie as input stream
(rgb :mov0 [c0 c1 c2 c3]
(sy 1.5)
(rgb c2.rgb)
)
(rgb :ras1 [mov0 ras1]
(rot (* ks1 0.3 (snoise x y)))
(sy (+ 0.95 (* ks2 0.1)))
(ty (+ -0.05 (* ks3 0.1)))
(rgb (mix mov0.rgb ras1.rgb 0.99))
)
(rgb :ras3 [ras1] (rgb (pow ras1.rgb (vec3 ks7 ks7 ks7))))
; ks1 0.46094
; ks2 0.92969
; ks3 0.64844
; ks7 0.32031
Droste Effekt
Dadurch, dass es jetzt einen (1) zusätzlichen Speicher im System gibt sind erhöhen sich die Möglichkeiten deutlich. Hier zum Beispiel der Droste-Effekt.
- Eine Kopie des Bildes im selben Bild platzieren.
- Diese Strategie wiederholt anwenden.

Diese ist einer der Effekte in der Loop - Camera.
https://metagrowing.org/loop?filter=F022
Mehrfach-Verkleinerungs-Kopier-Maschine
Die Säulen der fraktalen Geometrie: Rückkopplung und Iteration
Die Mehrfach-Verkleinerungs-Kopier-Maschine
in: Bausteine des Chaos von Peitgen, Jürgens, Saupe; circa 1992
- Der Verkleinerungs- und Duplizier-Vorgang liefert den Attraktor.
- Die originale Geometrie strebt gegen den Attraktor.
- Die Farben bleiben in etwa erhalten.
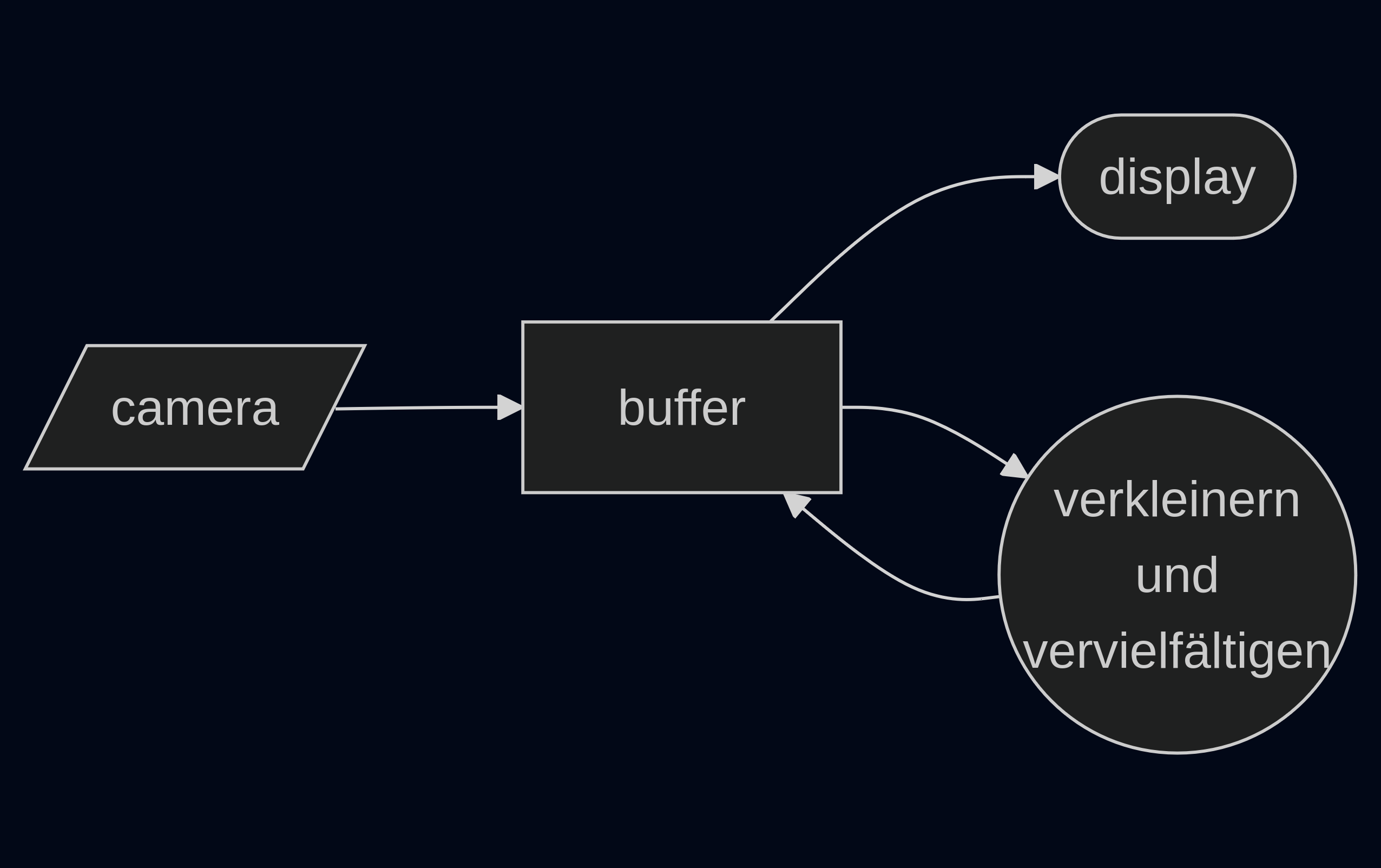

https://metagrowing.org/loop?cam=user&filter=F010
IFS/Flame mit Kamera oder Video Input
Kombination unterschiedlicher Ideen
- Punkte der Ebene immer wieder auf die Ebene abbilden. Eine ℝ² -> ℝ² Funktion wiederholt ausführen. Iteration
- Iterierte Funkionensysteme mit affinen Abbildungen als Ausgangspunkt. Barnsley Farn, Sierpinski-Dreieck ….
- Bei den geometrischen Transformationen Trigonometrie, Expotential-Funktionen, Polynome … zulassen. Wie bei Fractal Flames von Scott Davids.
- Die Farben aus der realen Welt nehmen.
Technisch: Von der schrittweisen seriellen Berechnung der ursprünglichen Iterierten Funkionensysteme auf eine hochgradig parallele Implementierung wechseln. 1 Million Punkte werden pro Frame jeweils um wenige Schritt transformiert.
Dann passt die ℝ² -> ℝ² Abbildung genau zur OpenGL Arithmetik: Vektoren als komplexe Zahlen.

- Die Geometrie wird von der wiedeholt ausgeführten Funktion bestimmt.
- Die Farben bleiben in etwa erhalten.
(ns lv.demo)
(use 'lv.core)
(layout "grid" [img0 igen1]
[ras2 ras3])
(image "flower-sampler/*.png")
(rgb :img0 [c0 c1 c2 c3]
(rgb (mix c3.rgb c2.rgb (usin (* 0.031 f))))
)
(expr :igen1 [ras3]
"r2/r2image.cl"
(p0 (* ks0 3))
(p1 (* (usin (* 0.007 f)) 3))
(p2 (* (usin (* 0.011 f)) 3))
(p3 (* (usin (* 0.013 f)) 3))
(p4 (* (usin (* 0.023 f)) 3))
(p7 (* ks7 3))
)
(rgb :ras2 [img0 igen1 ras2]
(rgb (mix (* 3 img0.rgb igen1.rgb) ras2.rgb 0.95))
)
(rgb :ras3 [img0 igen1]
(rgb (+ img0.rgb igen1.rgb))
)
(render)
float2 sinusoidal(float2 v, float amount) {
return amount * sin(v);
}
float2 spherical(float2 v, float amount) {
float r = length(v);
return (amount * 1.0f / (r * r)) * v;
}
float2 expotential(float2 v, float amount) {
return (amount * exp(v.x-1)) * (float2)(cos(M_PI_F*v.y), sin(M_PI_F*v.y));
}
#define a_index(ix,iy) (SX*iy + ix)
#define g_index(ix,iy) (2*SX*iy + 2 * ix)
__kernel void set_zero(
__global int* countersR,
__global int* countersG,
__global int* countersB
)
{
const int ix = get_global_id(0);
const int iy = get_global_id(1);
const int SX = get_global_size(0);
const int i_here = a_index(ix, iy);
countersR[i_here] = 0;
countersG[i_here] = 0;
countersB[i_here] = 0;
}
__kernel void map_r2(
__global int* countersR,
__global int* countersG,
__global int* countersB,
__read_only image2d_t image_in,
__global float* gaussian,
__global float* uniform,
const float p0,
const float p1,
const float p2,
const float p3,
const float p4,
const float p5,
const float p6,
const float p7,
const float dt0,
const float dt1,
const float dt2,
const float dt3,
const float dt4,
const float dt5,
const float dt6,
const float dt7
)
{
const int ix = get_global_id(0);
const int iy = get_global_id(1);
const int SX = get_global_size(0);
const int SY = get_global_size(1);
const int i_here = a_index(ix, iy);
sampler_t smp = CLK_ADDRESS_CLAMP_TO_EDGE | CLK_FILTER_NEAREST;
const float px = (float)ix / (float)SX;
const float py = (float)iy / (float)SY;
const float w0 = M_PI_F;
float2 pos = (float2)((2.0f*px-1) * w0,
(2.0f*py-1) * w0);
const float ga0 = p7 * 0.004;
const int g_here = g_index(ix, iy);
pos += ga0 * (float2)(gaussian[g_here], gaussian[g_here+1]);
for(uint l=0; l<7; ++l) {
pos = sinusoidal(pos, p0);
pos = spherical(pos, p1);
pos = expotential(pos, p2);
}
float2 out_pos = 0.5f + pos / ( w0 * 2);
int ox_pos = SX*out_pos.x;
int oy_pos = SY*out_pos.y;
if(ox_pos >= 0 && ox_pos < SX
&& oy_pos >= 0 && oy_pos < SY) {
const float4 color_in = read_imagef(image_in, smp, (int2)(ix, iy));
const int red = (int)(256*color_in.x);
const int green = (int)(256*color_in.y);
const int blue = (int)(256*color_in.z);
const int o_here = a_index(ox_pos, oy_pos);
atomic_add(&countersR[o_here], red);
atomic_add(&countersG[o_here], green);
atomic_add(&countersB[o_here], blue);
}
}
__kernel void write_image(
__global int* countersR,
__global int* countersG,
__global int* countersB,
__write_only image2d_t image2
)
{
const int ix = get_global_id(0);
const int iy = get_global_id(1);
const int SX = get_global_size(0);
const int i_here = a_index(ix,iy);
float red = countersR[i_here] > 0 ? tanh((float)(countersR[i_here]/256)) : 0;
float green = countersG[i_here] > 0 ? tanh((float)(countersG[i_here]/256)) : 0;
float blue = countersB[i_here] > 0 ? tanh((float)(countersB[i_here]/256)) : 0;
write_imagef(image2, (int2)(ix, iy), (float4)(red, green, blue, 1));
}
Conformal Map
“Winkeltreue” Abbildung der Ebene. Achtung: Dieses Bild ensteht ohne Rückkopplungsschleife.

https://metagrowing.org/glic?filter=F028
Zusätzlich eine externe Rückkopplung
Warum zusätzlich die externe Rückkopplung?
- Optische Effekte einsetzten die algorithmisch sehr aufwendig zu erzeugen sind.
- Eine Szene aus realen Gegenständen kann sehr einfach verändert werden.
- Erzeugt mit geringen Aufwand viele visuelle Details.
- Rein algorithmisch sieht zu “clean” aus.
Hilfsmittel
- Objekte und Gläser in der optischen Achse als zusätzlicher Filter.
- Lichtquellen als Initiator / Seed
- LEDs in der optischen Achse.
- Beleuchtung der Szene von außen. Denn eine Beleuchtung ausschließlich durch den Monitor funktioniert nicht.
- Der Algorithmus des Effektfilters dient als Initiator / Seed. Dabei beleuchtet der Monitor die Szene.
Monitor Spiegel Kamera Schleifen
Beispiele die mit externen Rückkopplung entstanden sind







Making of “light glass and mirrors”
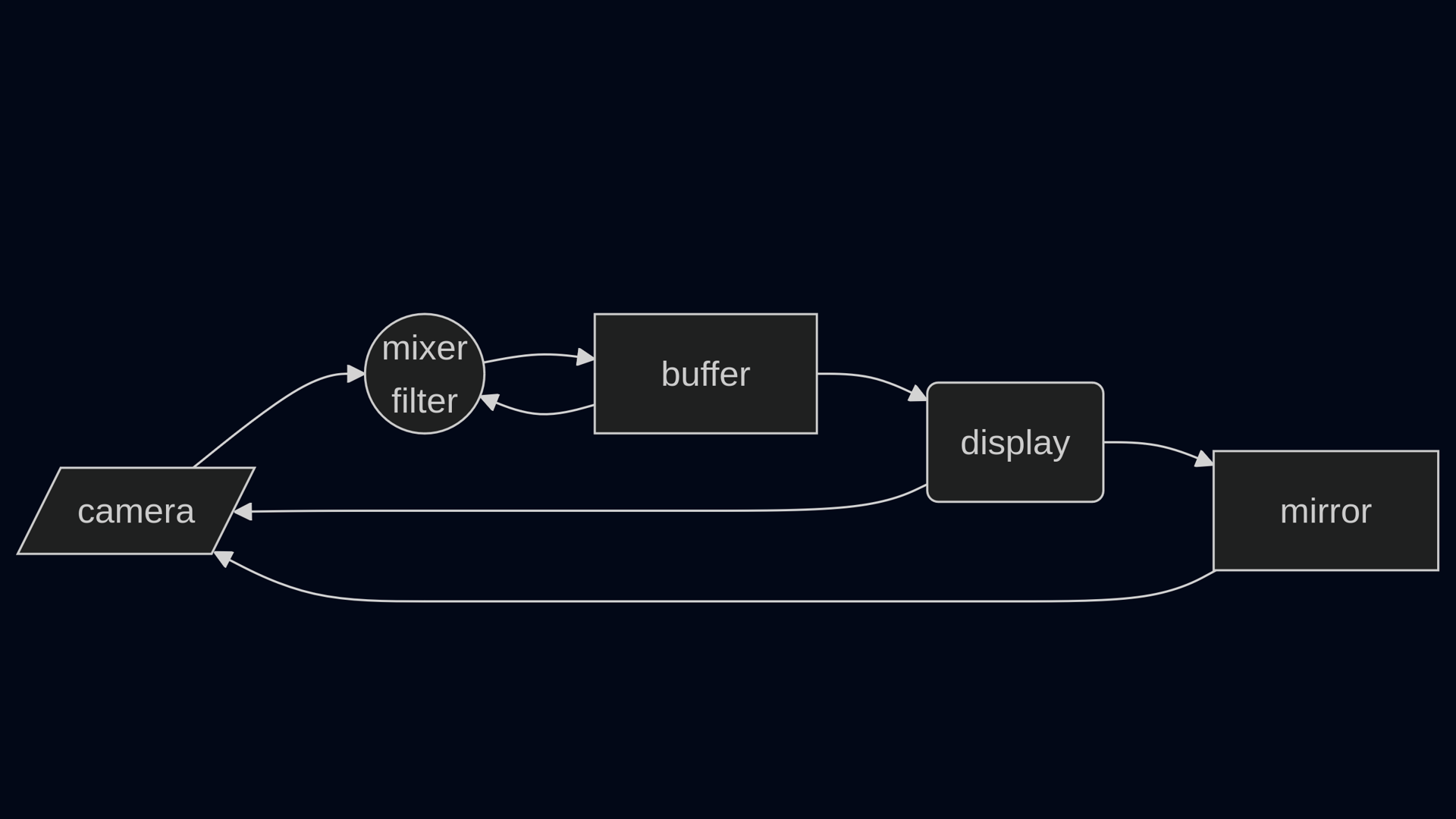 Es gibt mehrere Möglichkeiten das Bild abzugreifen.
Es gibt mehrere Möglichkeiten das Bild abzugreifen.
- Dies was die Kamera - die in die Schleife eingebunden ist - sieht.
- Dies was der Effektfilter anzeigt.
- Dies was eine zusätzliche Kamera sieht.



Externe contra interne Rückkopplung
extern analog einfach
- optische Brechung des Lichts
- Prismen, Gläser …
- Zeichnen mit Licht
- Flüssigkeiten
intern digital mit Hilfe von Algorithmen einfach
- Den Farbwinkel verändern
- Pixel Push / Pixel Sort Algorithmen
- audio-reaktiv
- Verzögerungsschleifen
- Bewegungserkennung
“Material” aus der realen Welt
Das Material erforschen um optische Stilmerkmale zu finden.
Materialien:
- Gläser
- Optische Brechung in Gläsern ausnutzen
- Farbige Gläser
- Lichtquellen
- direkt in der optischen Achse
- indirekte Beleuchtung
- Flüssigkeiten
- Ölfarbe auf Glasträger
- 2 unterschiedliche gefärbte Flüssigkeiten die sich nicht mischen.
- Wellenmuster in der Flüssigkeit
- mechanische Bewegungen
Stilistische Merkmale
Stilmerkmale analog und digital
Überlauf in den Farbkanälen
Bei analogen und digitalen Rückkopplungen kommt es schnell zu einem Überlauf der Farbkanäle.
In einem RGB System
- 1 Kanal übersteuert: rot oder grün oder blau dominiert.
- 2 Kanäle übersteuert: gelb oder cyan oder magneta dominiert.
- alle 3 Kanäle übersteuert: weiß
 Glitch Camera mit 8 Bit pro Farbkanal
Glitch Camera mit 8 Bit pro Farbkanal
Nicht unbedingt reproduzierbar
Digitale Systeme die Mitkopplungen / Rückkopplung enthalten sind nicht wesentlich leichter reproduzierbar als analoge Systeme mit Rückkopplung.
Der Vorzustand in den Rückkopplungspuffern beeinflusst das Ergebnis.
Bei analogen Systemen spielen zusätzlich elektromagnetische Einkopplungen, Temperatur der Elektronik, Kapazitäten, … eine Rolle.
 WebGL
WebGL
Stilmerkmale analog
Kamera Monitor Rotation
... piece was created using camera/LCD screen feedback ...
... rotated ...
.. camera was deliberately out of focus ...
Paloma Kop
FROM MATERIAL SPACE(TIME) TO ELECTRONIC SPACE(TIME): INTERFACES, SIMULATONS, HYBRIDIZATIONS
Page 20 https://palomakop.tv/mfa/
Formen
Analoge Rückkopplungen sind geeignet weiche und teilweise organische Muster zu erzeugen.

I processed the footage using Signal Culture's analog video
equipment, including a camera feedback loop, and the Jones
Colorizer, which was created by Dave Jones.
Paloma Kop, “Weird Things”, Analoge Ausrüstung
https://palomakop.tv/art/weird-things/
Farbabweichung
Beim betrachten ist der erste Eindruck, dass es sich um helles weißes Licht handelt. Aber da sind kleine blaue Spuren zu sehen. Es ist mir nicht klar was die blaue Farbabweichung verursacht.
 Paloma Kop, Analoge Ausrüstung, Projektion auf einen Wetterballon.
Paloma Kop, Analoge Ausrüstung, Projektion auf einen Wetterballon.
Die technische Grundlagen des analogen TV werden sichtbar.
Ein TV Signal besteht aus Frames. Frames bestehen aus Zeilen. Insofern ist die TV - Bildverarbeitung nicht vollständig analog. Dass es einzelne Scanlines gibt ist ein diskreter Aspekt. das kann man dann ausnützen in dem man den Elektronenstrahl des TV Monitors währen er die Scanlines zeichnet mit Magneten ablenkt.
Stilmerkmale digital
Fehlabtastung in der Textur-Einheit
Fehlabtastung in Textur-Einheit als Stilmittel. Hier Pixel Push ohne zusätzlichen Puffer.
Mit zusätzlichen Puffern wird Pixel Sort möglich.
 Glic-Camera WebGL
Glic-Camera WebGL
Rundungsfehler bei 8 Bit pro RGB Farbkanal.
Im linken oberen Quadrant sind Farbfehler zu sehen. Der Puffer für die interne Rückkopplung verwendet 8 Bit Integer.
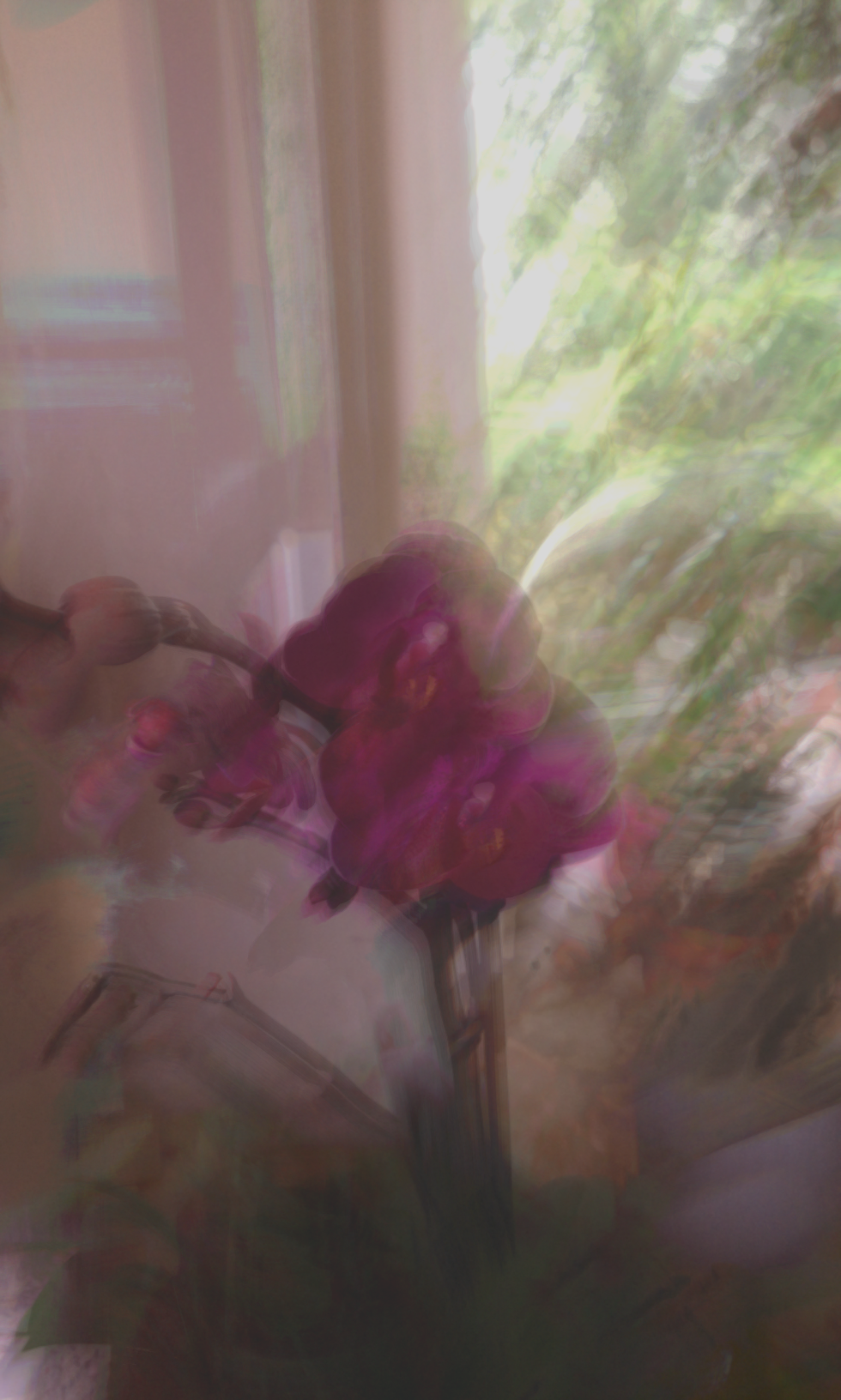 Loop-Camera WebGL mit 8 Bit pro Farbkanal.
Loop-Camera WebGL mit 8 Bit pro Farbkanal.
Geometrische Transformationen
Viele geometrische Transformationen der Bildebene sind möglich: Rotation, Translation, Affine Abbildung, Conformal Maps, Funktion mir komplexen Zahlen ….
 aNa als Kaleidoskop mit 32 Bit Floats pro Farbkanal
aNa als Kaleidoskop mit 32 Bit Floats pro Farbkanal
Kanten
Der digital Workflow erzeugt scharfe Kanten und (unerwünschtes) Aliasing.
Digital sieht es oft sehr “clean” aus. Diesen zu sauber glatten Eindruck kann man vermeiden: Als Input Material verwende, das in der realen Welt aufgenommen wurde. Oder in dem man auf eine strukturierte Oberfläche projiziert.
 aNa mit 8 Bit pro Farbkanal
aNa mit 8 Bit pro Farbkanal
Quellen
Paloma Kop “Weird Things”
https://palomakop.tv/art/weird-things/
https://videos.scanlines.xyz/w/a7Act8yFoP9g38jq1x6Hq9
Paloma Kop “EDGE OF LIGHT”
https://palomakop.tv/art/edge-of-light/
https://videos.scanlines.xyz/w/uJTa1bchqGCByWpQqDE7SS
Grenzen
Technische Grenzen
- Farbtiefe
- Übersteuern der Farbkanäle
- 8 Bit unsigned integer / 32 Bit Float pro Farbkanal
- Flackern
- Moinitor Tearing / vertical sync / V-RAM schreiben während das Bild an den Monitor übertragen wird.
- invertierende Filter können zu starken flackern führen.
- Sind die Algorithmen parallelisierbar?
- general purpose GPU / passen die Algorithmen ins “singel instruction multible data” (SIMD) Schema? Benötigte Zeit für die Berechnung
- 60 Hz -> 16 Millisekunden pro Frame
- 30 Hz -> 33 Millisekunden pro Frame
- Wie oft liefert die Kamera ein neues Bild, mit welcher Farbtiefe / Auflösung?
ungewollte Effekte
- LEDs werden gepulst betrieben.
- -> Puls Wellen Modulation contra geregeltem Gleichstrom
- Kamera mit automatischer Belichtung oder Auto-Fokus
- -> Externe Lichtquelle um flackern durch die Rückkopplung zu vermeiden
Software
DIY Software
analog Not analog / Clojure + openFrameworks
About analog Not analog https://metagrowing.org/ana/
aNa cookbook https://metagrowing.org/cookbook/
Glitch Camera / Smartphone
Kurz zeigen wie GLIC bedient wird.
Die Glitch Camera starten:
Beschreibung:
https://gitlab.com/metagrowing/glic
Loop Camera / Smartphone
Kurz zeigen wie LOOP bedient wird.
Die Loop Camera starten:
Beschreibung:
https://gitlab.com/metagrowing/loop
Alternative Software
WEB Cam Apps
Cheese, a tool to take pictures and videos from your webcam.

OBS Studio
OBS Studio kombiniert mit dem Kernel Modul v4l2loopback
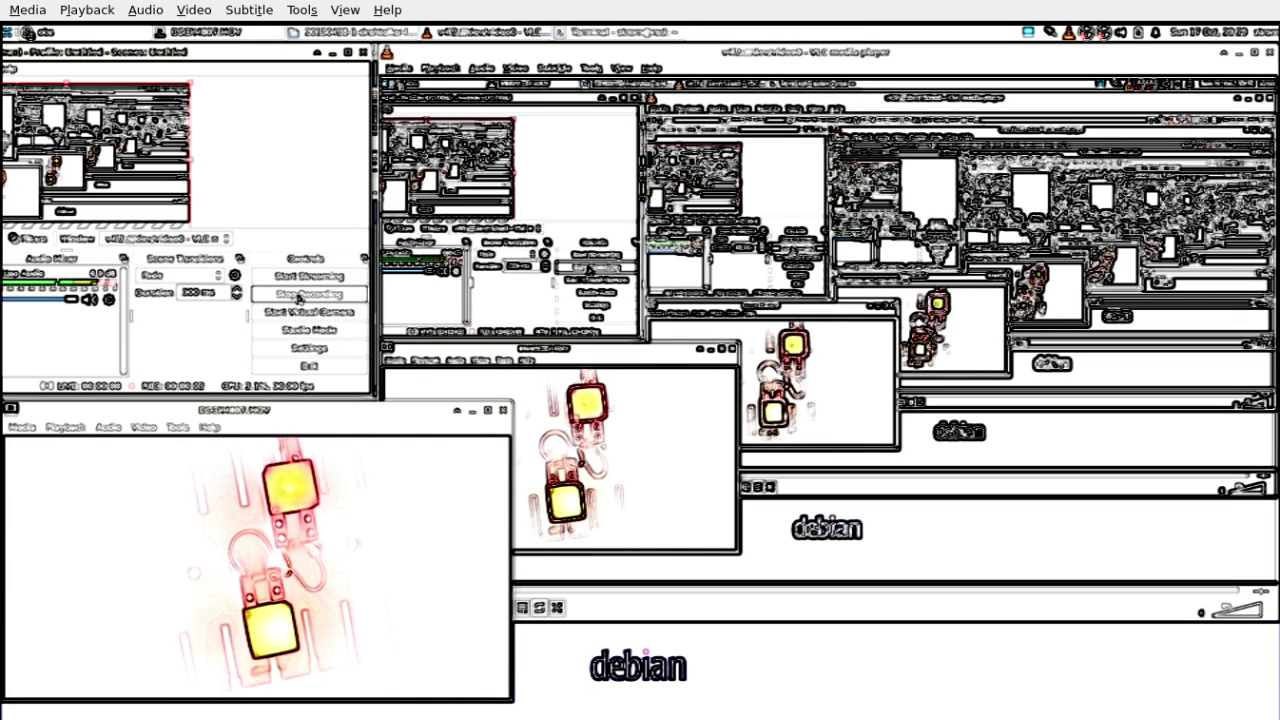
Hydra
Extra shaders for Hydra https://gitlab.com/metagrowing/extra-shaders-for-hydra

Links
analog Not analog
The ‘analog Not analog’ cookbook.
https://metagrowing.org/cookbook/
Source Code
https://gitlab.com/metagrowing/ana
Source Code for Examples
Loop Camera and Glitch Camera
https://gitlab.com/metagrowing/loop
https://gitlab.com/metagrowing/glic
Paloma Kop
MFA Thesis of Paloma Kop, Alfred University, 2020 https://palomakop.s3.us-east-1.amazonaws.com/palomakop_thesis_book_digital.pdf
scanlines.xyz community
mein Mastodon Kanal
© CC BY-NC-SA 4.0